采样与采样率
数字形式的音频是以离散形式存储的,采样率(Sampling rate)(Hz)决定了一秒内采样的次数,同样也会决定音频所能表示的最大频率(奈奎斯特极限,最大频率 = 采样率 / 2)
振幅与位深
采样率告诉我们多久采样一次,这两个数据则告诉我们,我们采样了什么 显然我们在高中时学过,振幅(Amplitude)可以体现响度,单位为dB
数字音频中,每个音频样本记录了音频波在某个时间的振幅,而位深则决定了描述此振幅值的准确度
与现实世界不同,在数字音频信号中,0dB是最大的可能振幅,所有其他的振幅都是负数。从经验上说,每减少6dB,振幅就减半,并且小于 -60dB 的声音通常是听不见的
位深(Depth)表示了将连续的振幅转化为离散值时,可以量化的可能步数,并且是二进制术语,例如16位音频为65536步。 量化涉及引入噪声,Depth越高,引入的噪声越小,常见的有16bit, 24bit
16bit, 24bit音频使用整数样本,但是32bit音频使用浮点值,32位浮点值的精度即为24位,使其与24bit音频有相同的depth
机器学习模型天生就处理浮点数据,所以音频要在转换为浮点格式后才能用于训练
作为波形的声音
声音以波形的形式可视化,可以绘制样本值随时间的变化,并说明了声音振幅的变化,也成为声音的 时域表示
可以使用python中的librosa库来显示波形
import librosaimport librosa.displayimport matplotlib.pyplot as plt
array, sampling_rate = librosa.load("J:\\MoeModels\\models\\Acro\\acro_wav\\ARU_M2_01_0026.wav")#返回一个含有音频样本的序列,和采样率组成的元组plt.figure().set_figwidth(12)librosa.display.waveshow(array, sr = sampling_rate)
plt.show()频谱
还可以使用频谱来绘制音频信号。频谱使用离散傅里叶变换(DFT)来计算,可以描述构成信号的各个频率和强度,使用numpy中的rfft()函数可以对声音进行DFT
import librosaimport librosa.displayimport matplotlib.pyplot as pltimport numpy as np
array, sampling_rate = librosa.load("J:\\MoeModels\\models\\Acro\\acro_wav\\ARU_M2_01_0026.wav")dft_input = array[:4096]#在这里剪切了音频的一部分用于绘图,实际上这是可有可无的
window = np.hanning(len(dft_input))#hanning返回一个钟形分布曲线(cosine bell)数组,参数决定了返回数组的长度#譬如[0, 0.1, ..., 1, ... , 0]#下文的连接有直观的图像windowed_input = dft_input * window#numpy中*运算即为数组(尺寸相同的)按位相乘,并且得到一个数组dft = np.fft.rfft(windowed_input)#对输入进行傅里叶变换
amp = np.abs(dft)#由于dft输出的是一个复数数组,所以需要使用abs()来对结果取模,来得到我们需要的振幅信息amp_db = librosa.amplitude_to_db(amp, ref=np.max)#这个函数正如其名,可以把刚刚得到的振幅信息转换为分贝刻度,方便我们观察频谱#np.max是librosa特有的语法,此时ref传入np.max函数,librosa会自行调用它,使ref = np.max(amp)#ref与振幅的缩放有关freq = librosa.fft_frequencies(sr = sampling_rate, n_fft=len(dft_input))#这一函数将确定频率的刻度,结合采样率后,我们可以将len(dft_input)这么多个点中任意一点对应哪个\#频率确定出来,譬如返回的第k个点代表的频率为(k * sr) / n_fft,返回值最大为sr / 2,也就是#先述的奈奎斯特频率#同时,需要注意返回数组的长度为1 + (n_fft / 2), 也就是0 <= k <= nfft / 2plt.figure().set_figwidth(12)plt.plot(freq, amp_db)#以freq为x轴,amp_db为y轴绘制图像,freq与amp_db形状相同,图像中任意一点的坐标为(freq_k, amp_db_k),其中k表示角标plt.xlabel("Frequency (Hz)")plt.ylabel("Amplitude (dB)")#为x,y轴命名plt.xscale("log")#将x轴的数值改为对数形式
plt.show()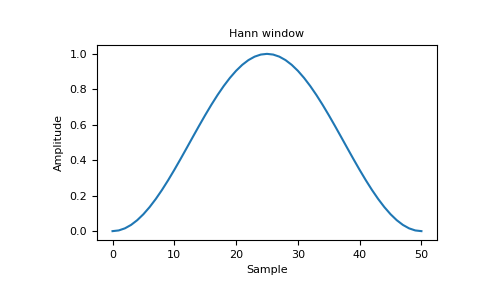
频谱图
频谱是在某一瞬间的音频频率分布,如果我们需要观察音频中频率如何变化,那么我们就需要进行多次DFT,每一次覆盖一小段时间,并把每次得到的频谱连接在一起,就得到了频谱图,可以借由此观察频率分布随时间的变化
关于瞬间: 可能你会注意到,在上一个示例代码中,我们使用了音频序列的前4096项,显然这并 不是一个瞬间,我们把一小段时间近似认为一个瞬间 生活也是如此,不是瞬间真的达到了,而是时间足够短了,以至于我们接受了(笑)
要得到频谱图,我们需要执行STFT,也就是短时傅里叶变换
import librosaimport librosa.displayimport matplotlib.pyplot as pltimport numpy as np
array, sampling_rate = librosa.load("J:\\MoeModels\\models\\Acro\\acro_wav\\ARU_M2_01_0026.wav")
dft = librosa.stft(array)#通过调用这一函数,我们可以同时完成对音频的切分,和对切分出的样本进行离散傅里叶变换#默认情况下,此函数会将音频分为2048个样本的片段sound_db = librosa.amplitude_to_db(np.abs(dft), ref=np.max)
plt.figure().set_figwidth(12)librosa.display.specshow(sound_db, x_axis="time", y_axis="hz")#使用这一函数来绘制频谱随时间变化的图像#可以注意到我们只传入了频率,我们不用再管x轴刻度的事,这个函数会帮我们做好plt.colorbar()#给频谱图上色,让我们更容易观察各个频率的强度,偏红为强,偏黑为弱
plt.show()
实际上,由于频谱图和波形是同一数据的不同视图,我们可以通过逆STFT将频谱图变为波形,要做到这个,除了振幅信息,我们还需要相位 为了得到相位,我们可以使用相位重建算法,或是声码器(一种神经网络),之后就可以重建波形了
除了用来可视化之外,许多机器学习模型会以频谱图为输入,并以频谱图为输出
梅尔频谱图
梅尔频谱图是一种频谱图变体,在标准频谱图中,频率轴是线性的,但是人耳的不同频率的听觉灵敏度随频率增加呈现对数下降,,所以我们有了梅尔频谱图,它的刻度是感知刻度,也就是非线性的 通过与之前一样使用STFT得到频谱,再对每个频谱进行滤波器处理,可以得到为梅尔频谱图, libsora.feature.melspectrogram() 会为我们做完这些事情
import librosaimport librosa.displayimport matplotlib.pyplot as pltimport numpy as np
array, sampling_rate = librosa.load("J:\\MoeModels\\models\\Acro\\acro_wav\\ARU_M2_01_0026.wav")
S = librosa.feature.melspectrogram(y = array, sr = sampling_rate)#输入一个声音序列是,会对其进行STFT并且返回梅尔频谱图#同时,可以不指定参数y,而是指定参数S,S为一个标准频谱图,在指定参数S时,这个函数会转换标准频谱图为梅尔频谱图S_db = librosa.power_to_db(S, ref=np.max)#由于melspectrogram()创建的梅尔频谱图是功率频谱图而非振幅,所以我们使用power_to_db()来得到分贝
plt.figure().set_figwidth(12)librosa.display.specshow(S_db, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)plt.colorbar()
plt.show()由于有了过滤信号的过程,所以创建梅尔频谱图是一个有损的过程 也因此,将梅尔频谱图转换为波形图需要估计被丢弃的频率,导致这一过程更加困难,也因此有了HiFiGAN这样的声码器来从梅尔频谱图生成波形
即使如此,梅尔频谱图可以捕获更多对人类感知有意义的音频信号特征,使其成为语音识别、说话人识别和音乐流派分类等任务中的热门选择
部分信息可能已经过时






